The core RedPRL Development Team (Carlo Angiuli, Evan Cavallo, Kuen-Bang Hou (Favonia), Reed Mullanix, and Jon Sterling) has developed several experimental proof assistants for Cartesian cubical type theory with the collaboration of Robert Harper. We are also building generic components and tools for modularly implementing proof assistants and elaborators.
The A.L.G.A.E. Project
We are developing composable (OCaml) libraries that facilitate the construction of a usable proof assistant from a core type checker. Currently, we are exploring the use of algebraic effects (instead of monads) to structure our libraries. So far, we have built these libraries specific to proof assistants:
- 🩺 asai: compiler diagnostics
- 📚 bantorra: library management
- ♾️ mugen: universe levels
- 📚 kado: cofibrations in Cartesian cubical type theory
- 👹 yuujinchou: hierarchical names and lexical scoping
We also have a few libraries for general purposes:
We have a prototype algaett (in progress) that demonstrates how to build a usable system using these libraries.Publications and talks
- Gratzer, S, A, Coquand, Birkedal. Controlling unfolding in type theory.
- F, A, M. An Order-Theoretic Analysis of Universe Polymorphism. POPL 2023.
- F. A Domain-Specific Language for Name Modifiers. TYPES 2022.
The cooltt proof assistant
We are currently developing cooltt, a prototype proof assistant for Cartesian cubical type theory, building on our previous work on the redtt proof assistant. cooltt supports systems for eliminating disjunctions of cofibrations, implementing the full definitional η-law.
Publications and talks
- S. Make Three To Throw Away: Frontiers in Homotopical Proof Assistants. Workshop on the Implementation of Type Systems (keynote).
We welcome new contributors!
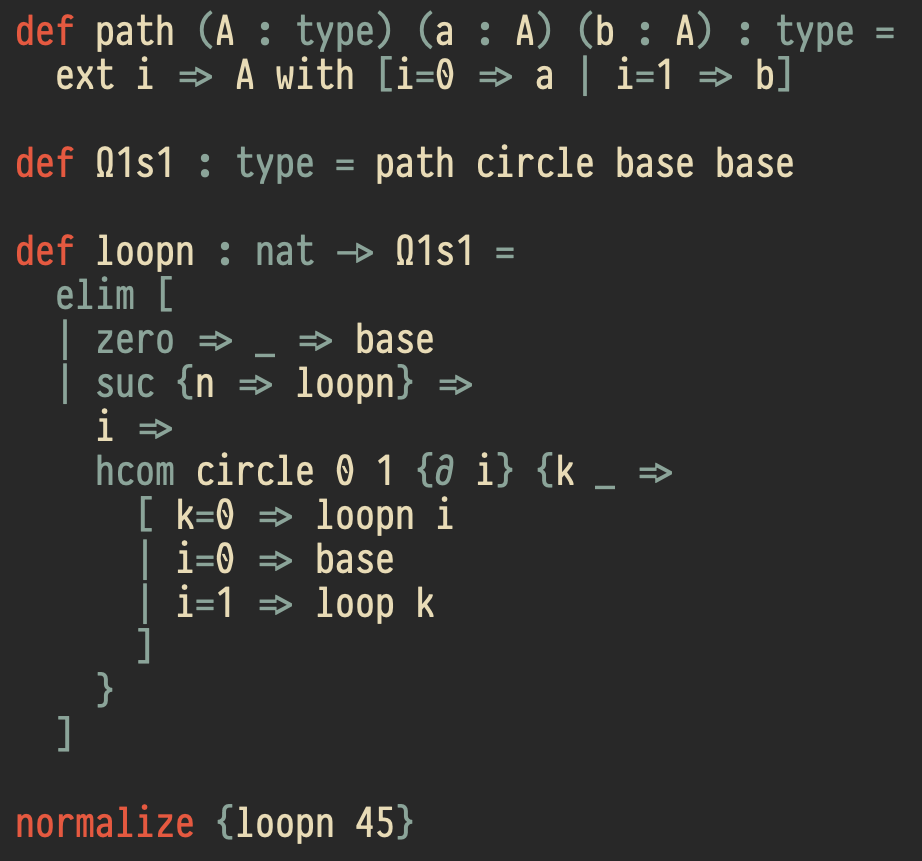
The redtt proof assistant
A proof assistant for Cartesian cubical type theory. Notable features include extension types, user-defined (parametric) higher inductive types, and rudimentary higher-order unification; redtt pioneered the boundary-sensitive treatment of holes that now appears in Cubical Agda and cooltt.
Publications and talks
- S. redtt and the future of Cartesian cubical type theory. Every proof assistant seminar.
- F. Towards Efficient Cubical Type Theory. Homotopy Type Theory Electronic Seminar Talks (HOTTEST).
- A, C, F, H, Mörtberg, S. redtt: implementing Cartesian cubical type theory. Dagstuhl Seminar 18341: Formalization of Mathematics in Type Theory.
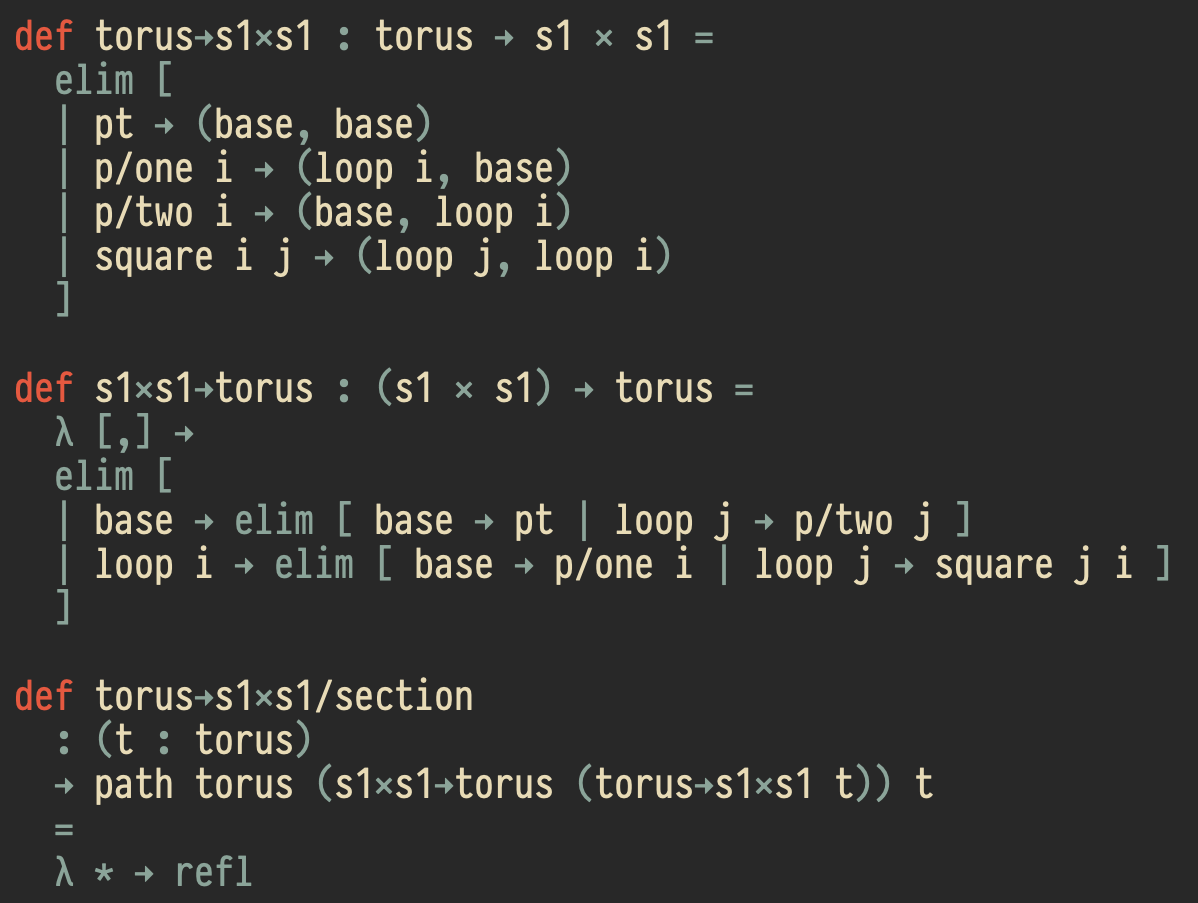
The RedPRL proof assistant
A tactic-based proof assistant for computational Cartesian cubical type theory inspired by Nuprl. RedPRL implements a two-level cubical type theory which includes univalent universes, some higher inductive types, and strict equality types with equality reflection.
Publications and talks
- A, C, F, H, S. The RedPRL Proof Assistant. LFMTP 2018.
- A, H. Computational Higher Type Theory. Tutorial at POPL 2018.

Acknowledgments
This research was sponsored by the Air Force Office of Scientific Research under grant number FA9550-15-1-0053 and the National Science Foundation under grant number DMS-1638352. We thank the Logic and Semantics Group at Aarhus University for their hospitality in during the summer of 2018, during which part of this work was undertaken. We also thank the Isaac Newton Institute for Mathematical Sciences for its support and hospitality during the program "Big Proof" when part of this work was undertaken; the program was supported by the Engineering and Physical Sciences Research Council under grant number EP/K032208/1. The views and conclusions contained here are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of any sponsoring institution, government or any other entity.